Série de Fourier
Rappel du cours d'Analyse Harmonique
Pour l'histoire, voilà un résumé très rapide de la vie de Joseph Fourier.
Vous avez déjà vu dans le cours d'Analyse Harmonique les séries de Fourier. Les séries de Fourier s'appliquent à des fonctions périodiques. Nous utiliserons la formulation complexe pour la série de Fourier.
Représentation fréquentielle :Joseph Fourier
Gravure de Julien Léopold Boilly (wikipedia)
Jean Baptiste Joseph Fourier, né le 21 mars 1768 à Auxerre et mort le 16 mai 1830 à Paris :
mathématicien et physicien français,
travaux sur la décomposition de fonctions périodiques en séries trigonométriques convergentes appelées séries de Fourier
application au problème de la propagation de la chaleur.
Définition : Série de Fourier : Formulation complexe
Soit f une fonction continue périodique de période T alors f peut s'écrire sous la forme :
\(f(t)=\sum_{n=-\infty}^{+\infty}c_ne^{i2\pi \frac{n}{T}t}\) avec \(c_n = \frac{1}{T}\int\limits_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-i2\pi \frac{n}{T}t}dt\)
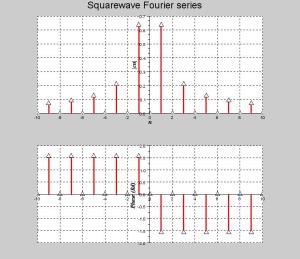
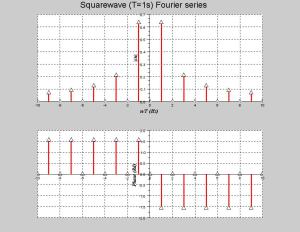
Exemple : Série de Fourier de la fonction périodique signal carré de période T
\(\sqcap_T (t)=1\) si \(kT\leq t\leq \frac{T}{2}+kT\) pour \(k\in Z\) et
\(\sqcap_T (t)=-1\) si \( \frac{T}{2}+kT < t < (k+1)T\) pour \(k\in Z\)
Calculons les coefficients cn de la série de Fourier en utilisant la définition précédente :
\(c_n = \frac{1}{T}\int\limits_{-\frac{T}{2}}^{\frac{T}{2}}\sqcap_T (t)e^{-i2\pi \frac{n}{T}t}dt\)
\(c_n = \frac{1}{T}\int\limits_{-\frac{T}{2}}^{0}{-e^{-i2\pi \frac{n}{T}t}dt}+\frac{1}{T}\int\limits_{0}^{\frac{T}{2}}e^{-i2\pi \frac{n}{T}t}dt\)
\(c_n = \frac{1}{T}\Bigg[\frac1{i\frac{2\pi n}{T}}e^{-i2\pi \frac{n}{T}t}\Bigg]_{-\frac{T}{2}}^{0}+\frac{1}{T}\Bigg[-\frac1{i\frac{2\pi n}{T}}e^{-i2\pi \frac{n}{T}t}\Bigg]_{0}^{\frac{T}{2}}\)
En simplifiant on obtient l'expression :
\(c_n =-\frac1{i 2\pi n}\Bigg(e^{-i\pi n}+e^{i\pi n}-2\Bigg)\)
En remarquant que \((a-b)^2=a^2-2ab+b^2\), l'expression précédente devient :
\(c_n =-\frac1{i 2\pi n}\Bigg(e^{-i\frac{\pi n}2}-e^{i\frac{\pi n}2}\Bigg)^2\) et finalement en utilisant la formule de Moivre on obtient :
\(c_n=\frac2{i\pi n}\sin^2\frac{\pi n}2\)
Finalement le signal carré peut s'écrire sous la forme :
\(f(t)=\cdot\cdot\cdot +c_{-2}e^{i2\pi t \frac{-2}{T}}+c_{-1}e^{i2\pi t \frac{-1}{T}}+c_{0}+c_{1}e^{i2\pi t\frac{1}{T}}+c_{2}e^{i2\pi t\frac{2}{T}}+\cdot\cdot\cdot\)
et en regroupant les termes judicieusement comme cela
\(f(t)=\cdot\cdot\cdot -\frac{2}{i\pi n}e^{i2\pi t\frac{-n}{T}}+\frac{2}{i\pi n}e^{i2\pi t\frac{n}{T}}+\cdot\cdot\cdot\)
on obtient
\(\sqcap_T(t)=\sum\limits_{k=0}^{+\infty}4\frac{\sin (2\pi (2k+1)\frac tT}{\pi (2k+1)}\)
On peut représenter graphiquement les coefficients \(c_n\) par deux graphiques, le premier est le module de \(c_n\) et le second l'argument de \(c_n\). En abscisses on a la valeur de n qui varie de \(-\infty\)à \(+\infty\). L'argument s'expriment en radian.
Plutôt que de mettre le coefficient n sur l'axe des abscisses, on peut mettre le coefficient \(\frac nT\). L'axe des abscisses est alors gradué en Hz.
Fondamental : Égalité de Parseval
Soit f une fonction périodique de période T admettant comme coefficients de Fourier cn. Les coefficients de la série de Fourier vérifient :
\(\frac 1{T}\int\limits_{\alpha}^{\alpha+T}|f(t)|^2dt=\sum\limits_{n=-\infty}^{+\infty}|c_n|^2\)
Remarque : Coefficient c0 de la série de Fourier
L'expression du coeffiecient de la série de Fourier en formulation complexe est :
\(c_n = \frac{1}{T} \int\limits_0^T {f(t) e^{-i2\pi n \frac{t}{T}} dt} \)
Pour obtenir, \(c_0 \),on remplace n par 0 on obtient donc :
\(c_0 = \frac{1}{T} \int\limits_0^T {f(t) dt} \)
On voit que c0 est alors la valeur moyenne de la fonction.